Turn on inline plotting
%matplotlib inline
import required packages
import pynamics
from pynamics.frame import Frame
from pynamics.variable_types import Differentiable,Constant
from pynamics.system import System
from pynamics.output import Output,PointsOutput
import pynamics.integration
import sympy
import numpy
import matplotlib.pyplot as plt
plt.ion()
from math import pi
import scipy.optimize
Create a pynamics system
system = System()
pynamics.set_system(__name__,system)
Declare constants
lA = Constant(2,'lA',system)
lB = Constant(1.5,'lB',system)
lC = Constant(1,'lC',system)
lD = Constant(1,'lD',system)
Create three differentiable state variables
qA,qA_d,qA_dd = Differentiable('qA',system)
qB,qB_d,qB_dd = Differentiable('qB',system)
qC,qC_d,qC_dd = Differentiable('qC',system)
qD,qD_d,qD_dd = Differentiable('qD',system)
Create an initial guess for their starting positions. Note that this is not necessarily accurate given the constraint that they are supposed to be connected with given, constant length. We will use these initial values to seed the solver that will find a valid initial state
initialvalues = {}
initialvalues[qA]=90*pi/180
initialvalues[qA_d]=0*pi/180
initialvalues[qB]=-90*pi/180
initialvalues[qB_d]=0*pi/180
initialvalues[qC]=5*pi/180
initialvalues[qC_d]=0*pi/180
initialvalues[qD]=90*pi/180
initialvalues[qD_d]=0*pi/180
Retrieve state variables in the order they are stored in the system
statevariables = system.get_state_variables()
Create four frames
N = Frame('N',system)
A = Frame('A',system)
B = Frame('B',system)
C = Frame('C',system)
D = Frame('D',system)
Declare N as the Newtonian (fixed) frame
system.set_newtonian(N)
Rotate A,B, and C about their local Z axes.
A.rotate_fixed_axis(N,[0,0,1],qA,system)
B.rotate_fixed_axis(A,[0,0,1],qB,system)
C.rotate_fixed_axis(N,[0,0,1],qC,system)
D.rotate_fixed_axis(C,[0,0,1],qD,system)
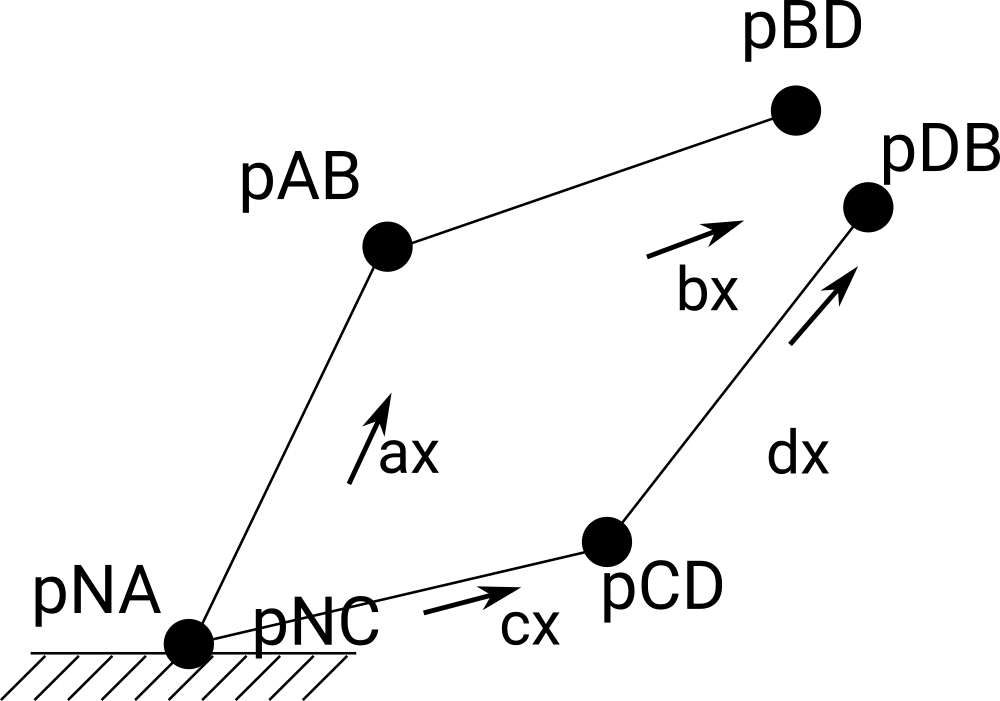
Define vectors that will be used to solve for kinematics. Note: this can be done several possible ways as in the figure below:
Define my rigid body kinematics
pNA = 0*N.x + 0*N.y + 0*N.z
pAB = pNA + lA*A.x
pBD = pAB + lB*B.x
pNC = pNA
pCD = pNC + lC*C.x
pDB = pCD + lD*D.x
type(pNA)
pynamics.vector.Vector
type(A)
pynamics.frame.Frame
type(A.x)
pynamics.vector.Vector
pout = pAB + 3*B.x-2*B.y
Declare a list of points that will be used for plotting
points = [pBD,pAB,pNA,pNC,pCD,pDB]
create a list of initial values ini0 in the order of the system’s state variables
statevariables = system.get_state_variables()
ini0 = [initialvalues[item] for item in statevariables]
Define the closed loop kinematics of the four bar linkage.
eq_vector = [pBD-pDB]
Dot the vector equation with N.x and N.y to create two scalar equations. This will remove two degrees of freedom from our system.
eq_scalar = []
eq_scalar.append((eq_vector[0]).dot(N.x))
eq_scalar.append((eq_vector[0]).dot(N.y))
eq_scalar.append(qC-0)
eq_scalar
[lA*cos(qA) - lB*sin(qA)*sin(qB) + lB*cos(qA)*cos(qB) - lC*cos(qC) + lD*sin(qC)*sin(qD) - lD*cos(qC)*cos(qD), lA*sin(qA) + lB*sin(qA)*cos(qB) + lB*sin(qB)*cos(qA) - lC*sin(qC) - lD*sin(qC)*cos(qD) - lD*sin(qD)*cos(qC), qC]
Solve for valid initial condition determined by independent variable
identify independent and dependent variables
qi = [qA]
qd = [qB,qC,qD]
for dependent variables, create an initial guess
substitute constants into the scalar equations
eq_scalar_c = [item.subs(system.constant_values) for item in eq_scalar]
Create a dictionary for all independent variables and substitute in
defined = dict([(item,initialvalues[item]) for item in qi])
eq_scalar_c = [item.subs(defined) for item in eq_scalar_c]
eq_scalar_c
[-1.5*sin(qB) + sin(qC)*sin(qD) + 9.18485099360515e-17*cos(qB) - cos(qC)*cos(qD) - cos(qC) + 1.22464679914735e-16, 9.18485099360515e-17*sin(qB) - sin(qC)*cos(qD) - sin(qC) - sin(qD)*cos(qC) + 1.5*cos(qB) + 2.0, qC]
convert to numpy array and sum the error
error = (numpy.array(eq_scalar_c)**2).sum()
Convert to a function that scipy can use. Sympy has a “labmdify” function that evaluates an expression, but scipy needs a slightly different format.
f = sympy.lambdify(qd,error)
def function(args):
return f(*args)
Take the derivative of the equations to linearize with regard to the velocity variables
guess = [initialvalues[item] for item in qd]
result = scipy.optimize.minimize(function,guess)
if result.fun>1e-3:
raise(Exception("out of tolerance"))
ini = []
for item in system.get_state_variables():
if item in qd:
ini.append(result.x[qd.index(item)])
else:
ini.append(initialvalues[item])
points = PointsOutput(points, constant_values=system.constant_values)
points.calc(numpy.array([ini0,ini]),numpy.array([0,1]))
points.plot_time()
2022-02-19 17:23:17,233 - pynamics.output - INFO - calculating outputs
2022-02-19 17:23:17,234 - pynamics.output - INFO - done calculating outputs
<AxesSubplot:>
result.fun
2.3019345538191714e-14
Consider Constraint Equations
$$ 0 = \left[\begin{array}{c} f_1(q_1,...q_n) \\ \vdots\\ f_m(q_1,...q_n) \end{array}\right]$$Take the derivative
$$ 0 = \left[\begin{array}{c} \dot{f}_1(q_1,...q_n) \\ \vdots\\ \dot{f}_m(q_1,...q_n) \end{array}\right]=\underbrace{\left[\begin{array}{ccc} j_{1q_1} & \dots & j_{1q_n} \\ \vdots & \ddots & \vdots \\ j_{mq_1} & \dots & j_{mq_n} \end{array}\right]}_{J_{c}}\left[\begin{array}{c} \dot{q}_1\\\vdots\\\dot{q}_n\end{array}\right]$$eq_d=[(system.derivative(item)) for item in eq_scalar]
eq_d = sympy.Matrix(eq_d)
eq_d = eq_d.subs(system.constant_values)
eq_d
Matrix([
[qA_d*(-1.5*sin(qA)*cos(qB) - 2*sin(qA) - 1.5*sin(qB)*cos(qA)) + qB_d*(-1.5*sin(qA)*cos(qB) - 1.5*sin(qB)*cos(qA)) + qC_d*(sin(qC)*cos(qD) + sin(qC) + sin(qD)*cos(qC)) + qD_d*(sin(qC)*cos(qD) + sin(qD)*cos(qC))],
[qA_d*(-1.5*sin(qA)*sin(qB) + 1.5*cos(qA)*cos(qB) + 2*cos(qA)) + qB_d*(-1.5*sin(qA)*sin(qB) + 1.5*cos(qA)*cos(qB)) + qC_d*(sin(qC)*sin(qD) - cos(qC)*cos(qD) - cos(qC)) + qD_d*(sin(qC)*sin(qD) - cos(qC)*cos(qD))],
[ qC_d]])
Now, given a valid configuration, solve for the linearized, velocity-based constraint equation. If
$$0= \textbf{J}_c \dot{q} = \textbf{A} \dot{q}_i + \textbf{B} \dot{q}_d$$
where $\textbf{A}_{(m \times (n-m))}$, $\textbf{B}_{(m \times m)}$
$$\dot{q}=\left[\begin{array}{c} \dot{q}_{i1} \\ \vdots \\ \dot{q}_{i(n-m)}\\ \hline \dot{q}_{d1}\\ \vdots\\ \dot{q}_{dm} \end{array}\right]$$Define independent variables as a Sympy Matrix
qi = sympy.Matrix([qA_d])
qi
Matrix([[qA_d]])
Define dependent variables as a Sympy Matrix
qd = sympy.Matrix([qB_d,qC_d,qD_d])
qd
Matrix([
[qB_d],
[qC_d],
[qD_d]])
take partial derivative of constraints with respect to independent and dependent variables:
AA = eq_d.jacobian(qi)
AA
Matrix([
[-1.5*sin(qA)*cos(qB) - 2*sin(qA) - 1.5*sin(qB)*cos(qA)],
[-1.5*sin(qA)*sin(qB) + 1.5*cos(qA)*cos(qB) + 2*cos(qA)],
[ 0]])
BB = eq_d.jacobian(qd)
BB
Matrix([
[-1.5*sin(qA)*cos(qB) - 1.5*sin(qB)*cos(qA), sin(qC)*cos(qD) + sin(qC) + sin(qD)*cos(qC), sin(qC)*cos(qD) + sin(qD)*cos(qC)],
[-1.5*sin(qA)*sin(qB) + 1.5*cos(qA)*cos(qB), sin(qC)*sin(qD) - cos(qC)*cos(qD) - cos(qC), sin(qC)*sin(qD) - cos(qC)*cos(qD)],
[ 0, 1, 0]])
Solve the internal input/output Jacobian to find $q_d$
$$0= \textbf{A} \dot{q}_i + \textbf{B} \dot{q}_d$$ $$-\textbf{B}\dot{q}_d = \textbf{A}\dot{q}_i$$ $$\dot{q}_d = \underbrace{-\textbf{B}^{-1}\textbf{A}}_{C}\dot{q}_i$$J_int= -BB.inv()*AA
J_int
Matrix([
[-(-1.5*sin(qC)*sin(qD) + 1.5*cos(qC)*cos(qD))*(-1.5*sin(qA)*cos(qB) - 2*sin(qA) - 1.5*sin(qB)*cos(qA))/(-2.25*sin(qA)*sin(qB)*sin(qC)*cos(qD) - 2.25*sin(qA)*sin(qB)*sin(qD)*cos(qC) + 2.25*sin(qA)*sin(qC)*sin(qD)*cos(qB) - 2.25*sin(qA)*cos(qB)*cos(qC)*cos(qD) + 2.25*sin(qB)*sin(qC)*sin(qD)*cos(qA) - 2.25*sin(qB)*cos(qA)*cos(qC)*cos(qD) + 2.25*sin(qC)*cos(qA)*cos(qB)*cos(qD) + 2.25*sin(qD)*cos(qA)*cos(qB)*cos(qC)) - (1.5*sin(qC)*cos(qD) + 1.5*sin(qD)*cos(qC))*(-1.5*sin(qA)*sin(qB) + 1.5*cos(qA)*cos(qB) + 2*cos(qA))/(-2.25*sin(qA)*sin(qB)*sin(qC)*cos(qD) - 2.25*sin(qA)*sin(qB)*sin(qD)*cos(qC) + 2.25*sin(qA)*sin(qC)*sin(qD)*cos(qB) - 2.25*sin(qA)*cos(qB)*cos(qC)*cos(qD) + 2.25*sin(qB)*sin(qC)*sin(qD)*cos(qA) - 2.25*sin(qB)*cos(qA)*cos(qC)*cos(qD) + 2.25*sin(qC)*cos(qA)*cos(qB)*cos(qD) + 2.25*sin(qD)*cos(qA)*cos(qB)*cos(qC))],
[ 0],
[ -(1.0*sin(qA)*sin(qB) - 1.0*cos(qA)*cos(qB))*(-1.5*sin(qA)*cos(qB) - 2*sin(qA) - 1.5*sin(qB)*cos(qA))/(1.0*sin(qA)*sin(qB)*sin(qC)*cos(qD) + 1.0*sin(qA)*sin(qB)*sin(qD)*cos(qC) - 1.0*sin(qA)*sin(qC)*sin(qD)*cos(qB) + 1.0*sin(qA)*cos(qB)*cos(qC)*cos(qD) - 1.0*sin(qB)*sin(qC)*sin(qD)*cos(qA) + 1.0*sin(qB)*cos(qA)*cos(qC)*cos(qD) - 1.0*sin(qC)*cos(qA)*cos(qB)*cos(qD) - 1.0*sin(qD)*cos(qA)*cos(qB)*cos(qC)) - (-1.0*sin(qA)*cos(qB) - 1.0*sin(qB)*cos(qA))*(-1.5*sin(qA)*sin(qB) + 1.5*cos(qA)*cos(qB) + 2*cos(qA))/(1.0*sin(qA)*sin(qB)*sin(qC)*cos(qD) + 1.0*sin(qA)*sin(qB)*sin(qD)*cos(qC) - 1.0*sin(qA)*sin(qC)*sin(qD)*cos(qB) + 1.0*sin(qA)*cos(qB)*cos(qC)*cos(qD) - 1.0*sin(qB)*sin(qC)*sin(qD)*cos(qA) + 1.0*sin(qB)*cos(qA)*cos(qC)*cos(qD) - 1.0*sin(qC)*cos(qA)*cos(qB)*cos(qD) - 1.0*sin(qD)*cos(qA)*cos(qB)*cos(qC))]])
That expression is quite long. We can use the simplify function provided by sympy to shorten the expression:
J_int.simplify()
J_int
Matrix([
[1.33333333333333*sin(-qA + qC + qD)/sin(qA + qB - qC - qD) - 1.0],
[ 0],
[ 2.0*sin(qB)/sin(qA + qB - qC - qD)]])
Solving for the dependent variables $q_d$:
Apply to end-effector
$$\textbf{v}_{out} = \textbf{J}\dot{\textbf{q}}$$ $$\textbf{v}_{out} = \textbf{D}\dot{\textbf{q}}_i+\textbf{E}\dot{\textbf{q}}_d$$ $$\textbf{v}_{out} = \textbf{D}\dot{\textbf{q}}_i+\textbf{EC}\dot{\textbf{q}}_i$$ $$\textbf{v}_{out} = \textbf{(D+EC)}\dot{\textbf{q}}_i$$Pick an end-effector
pout
lA*A.x + 3*B.x - 2*B.y
vout = pout.time_derivative()
#vout = vout.subs(subs)
vout = sympy.Matrix([vout.dot(N.x),vout.dot(N.y)])
vout
Matrix([
[-lA*qA_d*sin(qA) - ((2*qA_d + 2*qB_d)*sin(qB) + (3*qA_d + 3*qB_d)*cos(qB))*sin(qA) + ((2*qA_d + 2*qB_d)*cos(qB) - (3*qA_d + 3*qB_d)*sin(qB))*cos(qA)],
[ lA*qA_d*cos(qA) + ((2*qA_d + 2*qB_d)*sin(qB) + (3*qA_d + 3*qB_d)*cos(qB))*cos(qA) + ((2*qA_d + 2*qB_d)*cos(qB) - (3*qA_d + 3*qB_d)*sin(qB))*sin(qA)]])
Ji = vout.jacobian(qi)
Ji
Matrix([
[-lA*sin(qA) + (-3*sin(qB) + 2*cos(qB))*cos(qA) + (-2*sin(qB) - 3*cos(qB))*sin(qA)],
[ lA*cos(qA) + (-3*sin(qB) + 2*cos(qB))*sin(qA) + (2*sin(qB) + 3*cos(qB))*cos(qA)]])
Jd = vout.jacobian(qd)
Jd
Matrix([
[(-3*sin(qB) + 2*cos(qB))*cos(qA) + (-2*sin(qB) - 3*cos(qB))*sin(qA), 0, 0],
[ (-3*sin(qB) + 2*cos(qB))*sin(qA) + (2*sin(qB) + 3*cos(qB))*cos(qA), 0, 0]])
J = Ji+Jd*J_int
J
Matrix([
[-lA*sin(qA) + ((-3*sin(qB) + 2*cos(qB))*cos(qA) + (-2*sin(qB) - 3*cos(qB))*sin(qA))*(1.33333333333333*sin(-qA + qC + qD)/sin(qA + qB - qC - qD) - 1.0) + (-3*sin(qB) + 2*cos(qB))*cos(qA) + (-2*sin(qB) - 3*cos(qB))*sin(qA)],
[ lA*cos(qA) + ((-3*sin(qB) + 2*cos(qB))*sin(qA) + (2*sin(qB) + 3*cos(qB))*cos(qA))*(1.33333333333333*sin(-qA + qC + qD)/sin(qA + qB - qC - qD) - 1.0) + (-3*sin(qB) + 2*cos(qB))*sin(qA) + (2*sin(qB) + 3*cos(qB))*cos(qA)]])