$$ \frac{ {}^N{d\vec{v}}}{dt} = \frac{ {}^A{d\vec{v}}}{dt} + {}^N{\vec{w}}^{A} \times \vec{v} $$
Example
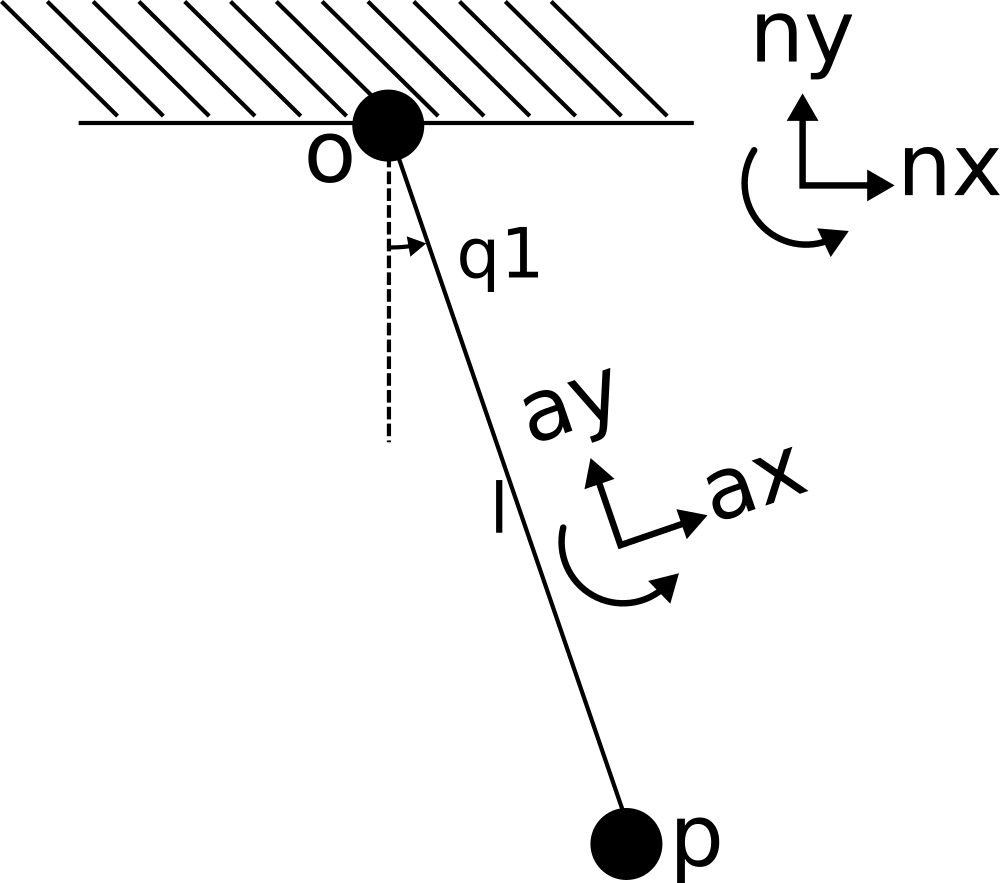
$$ \vec{r} = -l\hat{a}_y $$ $$ \vec{v} = \frac{ {}^N{d\vec{r}}}{dt} =\frac{ {}^{A} { d\vec{r}}}{dt} + {}^{N}{\vec{\omega}}^{A} \times \vec{r} $$ $$ \vec{v} = \frac{ {}^{N}{d\vec{r}}}{dt} = \dot{\theta}\hat{a}_z \times -l\hat{a}_y $$ $$ \vec{v} = \frac{ {}^{N}{}{ d\vec{r}}{}{}}{dt}= l\dot{\theta}\hat{a}_x $$ $$ \vec{a} = \frac{ {}^{N}{}{ d\vec{v}}{}{}}{dt} = \frac{ {}^{N}{}{d^2\vec{r}}{}{}}{dt^2} $$ $$ \vec{a} = \frac{ {}^{A}{}{d\vec{v}}{}{}}{dt} + {}^{N}{}{\vec{\omega}}^{A}{} \times \vec{v} $$ $$ \vec{a} = l\ddot{\theta}\hat{a}_x + \dot{\theta}\hat{a}_z \times l\dot{\theta}\hat{a}_x $$ $$ \vec{a} = l\ddot{\theta}\hat{a}_x + l\dot{\theta}^2\hat{a}_y $$
Frame A
- $ {}^{N}{}{\vec{\omega}}^{A}{} = \dot{\theta} \hat{n}_z= \dot{\theta} \hat{a}_z$